Search
As of October, 2016, Embarcadero is offering a free release
of Delphi (Delphi
10.1 Berlin Starter Edition ). There
are a few restrictions, but it is a welcome step toward making
more programmers aware of the joys of Delphi. They do say
"Offer may be withdrawn at any time", so don't delay if you want
to check it out. Please use the
feedback link to let
me know if the link stops working.
Support DFF - Shop
If you shop at Amazon anyway, consider
using this link.
We receive a few cents from each
purchase. Thanks
Support DFF - Donate
If you benefit from the website, in terms of
knowledge, entertainment value, or something otherwise useful,
consider making a donation via PayPal to help defray the
costs. (No PayPal account necessary to donate via credit
card.) Transaction is secure.
Mensa®
Daily Puzzlers
For over 15 years
Mensa Page-A-Day calendars have provided several puzzles a year
for my programming pleasure. Coding "solvers" is most fun,
but many programs also allow user solving, convenient for "fill
in the blanks" type. Below are Amazon links to the
two most recent years.
Mensa®
365 Puzzlers Calendar 2017
Mensa®
365 Puzzlers Calendar 2018

(Hint: If you can
wait, current year calendars are usually on sale in January.)
Contact
Feedback:
Send an
e-mail with your comments about this program (or anything else).
|
| |
| |
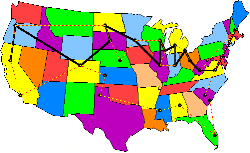
Problem Description
The Traveling Salesman Problem (TSP) requires
that we find the shortest path visiting each of a given set of cities
and returning to the starting point. Here's a program that lets you
match your skill against the computer to define a path connecting a random
set of U.S. cities.
Background & Techniques
I want to thank fellow seeker Robert Harrold for suggesting this
project. He runs a wide ranging website including this
education page where he was kind enough to place a link to DFF. He says that a computer display similar to
this program existed on the second floor of the National Aerospace
Museum in Washington, DC during the 80's. It disappeared one day in
1988, and he's been looking for it ever since. Maybe this will
help, Bob. Thanks for asking.
TSP belongs to a class of problems which for some non-obvious reason
are called NP complete. These
problems have no known efficient algorithms for solving them.
"Not efficient" here means that the time to solve the problem increases
exponentially with problem size, i.e. time to solve is an expression that
contains N as an exponent. This is a much faster growth
rate than any polynomial time problem. (Compare values of N2
and 2N for N=2, 10, 20 and 30 to see the effect of exponential
growth in the simplest case.)
There seems to be a lot of ongoing research on efficient techniques for solving
TSP - the first
solution of a 15,000 city case was just found in 2001, up dramatically
from the landmark 49 city solution found in 1954. There are
other applications of the TSP beyond salesmen and school busses.
For example: robotic travel problems like soldering or
drilling operations on printed circuit boards, sequencing local genome
maps to produce a global map, planning the order in which a satellite
interferometer studies a sequence of stars, etc. A Google search will turn up lots
more. Perhaps as important as the direct applications, TSP
provides a base for academic research on discrete optimization
problems. It's definitely intriguing that a problem so easy to state
can be so difficult to solve.
Exhaustive search breaks down at something
less than 15 cities (about a trillion, 1012, paths to check).
When the number of cities exceeds the low teens, we'll have to rely on heuristic
(rule of thumb) techniques which provide "pretty good" or
"good enough" solutions.
This program shows a map the 48 contiguous USA
states and lets you generate a set of up to 50 cities and click them
to form a path with your mileage totaled. There are both
exhaustive search and heuristic technique buttons provided for the
computer path search.
Non-programmers are welcome to read on, but
may want to skip to the bottom of
the page now to download the executable version of TSP.
Programmers Notes:
For an advanced program, there were surprisingly few hard problems to
solve here. Total development time was about 3 days, helped
considerably by the fact that the actual path search code already existed.
 | I found an outline map of the US on the web
and used that as the base map as file USA.bmp. I
load it into a a separate bitmap control in the program so that it can
be used to refresh the image as required. I
should probably have converted the file to a resource in our TSP.res
resource file, but laziness set in. |
 | Cities are defined at the nearest 10 pixel
boundary. This makes it practical to keep the city
information in a TStringlist with a string version of the
coordinates (8 characters XXXXYYYY) as the key. This make
it fast and easy to check if the mouse is on a city as it moves over
the image. One disadvantage: if the image size
were to be changed, city coordinates would have to be reentered, or at
least rescaled. Many more cities could be entered.
There is a Define Cities button which will pop up a dialog to
enter a city name when the mouse is clicked. A
simple object, TCoordObj, is used to hold city name, the
coordinates in integer form, and a Visited flag used to avoid
revisiting cities already in a path. A list, including a string
version of the TCoordObj object, is saved as a stream file
named CityList.str, used at startup time to
initialize the list of available cities. |
 | Scaling of distances traveled is accomplished
by converting pixel distance to miles with a miles per pixel scaling
factor, Scale. Scale is set by
computing the pixel distance between New York City and Los Angeles and
assuming the distance is 3000 miles. (Accuracy is not a big
concern here.) If either city is not found, Scale
is set to 6.7335. |
 | User define their path by clicking on cities
in order to be visited. OnMouseUp exit detects that we are
drawing a path and, if on an unvisited city, add the city to a ListToShow
stringlist. |
 | The "Exhaustive search" code here
was lifted from my Fences and
Traveling Salesmen program. It uses the Combo unit to
generate permutations of N numbers, each representing a potential
route. |
 | Pascal code for the heuristic methods was
downloaded from a page at the Stony
Brook Algorithm Repository Heuristics used are
called "Furthest insertion", "Two level exchange",
"Three level exchange" and are posted from the book Discrete
Optimization Algorithms with Pascal Programs by Maciej M. Syslo,
Narsingh Deo, and Janusz S. Kowalik. Unfortunately the
book is out of print and the only used copy available at Amazon.com has
an asking price of $100! About the heuristics themselves, I
know not much more than their names. I tried one called
"Branch and Bound" which worked for small cases but
causes range check exceptions for larger ones. The
commented code is still in the program for others to work on.
One more note - the heuristics seem to be tailored for closed paths,
i.e. unchecking the "Round trip" checkbox results in
paths that are pretty easy to beat. |
Well, as usual, time is short, life is fleeting,
and I have miles to go before I sleep. So let's get on with it!
Addendum December 18, 2009: It has
been 7 years since the original posting, time for an update, prompted by a
user request for the ability to specify the starting city for open paths
(visit all cities, but no need to return to the starting point). The
original version always started at the western-most city displayed.
Version 2 starts open path searches at the first city specified by the
user.
September 7, 2011: For the past month
or so I have been "working" on converting the TSP program to use
latitude/longitude instead of pixel coordinates to locate cities and measure
distances. There are still a number of features I
would like to add, but it's time to take a break and publish what works
leaving the rest as items for "Future Explorations". Here's a summary
of changes in TSP Version 3.
Mercator Projections: In order to accurately overlay cities on a
flat map based on their lat/long coordinates, we need a map with known
scaling. I chose the most popular, the Mercator projection, which maps
the earth onto a cylinder with its vertical axis through the poles and its
diameter matching the earth's diameter at the equator. Points above
and below the equator are "stretched" to lie on the cylinder, like a balloon
blown inside of a cylinder. if we then sliced the cylinder vertically
along the prime meridian, the 0 degree latitude line, and "unroll" it, we
have a flat map representation of the earth. Places near the poles get
"stretched" more than those nearer the equator and, in fact, generally are
not considered usable at more than 85 degrees North or South Latitudes.
Countries near the equator object to the fact that the Mercator projection makes them
seem smaller than they actually are in relation to countries further
north or south, which is true. But it seems that the advantages
and widespread use of Mercator projections have been enough to over come
those objections.
I found a Mercator outline map of the US to replace
the one used here previously. The "MakeCityLocations" program
posted a few weeks ago, provides us with a file of selected US Cities with
lat/long coordinates. The first two records in the file contain
diagonally separated locations which the user must locate on the
map image with mouse clicks. on a one time basis. These
points are saved in a init file, TSP3.ini, for future executions
The Lat/Long and the pixel coordinates for two cities is enough to let us
scale all of the other cities on the map.
TSP3.INI file: INI files predate the Windows registry as a place
to save information from run to run of a program. TSP3.INI currently
contains the names and pixel coordinates of the two points used to establish
conversion factors for converting Lat/Long to pixel coordinates.
This file also contains the last used names of the map file and the
cities list file.
Defining User Itineraries: Users may now click the "Define User Itinerary" radio button and define
their own set of cities to be visited. Cities may be selected by
clicking the city as its name is displayed as the mouse hovers over it.
Selected cities are displayed in red. Clicking on a city already added
will remove it from the itinerary. Right click anywhere to signal the
set is complete. If the "Round trip" checkbox is not checked, the
initial city will display as a red dot. (For round trips, the initial
city does not affect the shortest route distance.)
Defining User Paths: When an itinerary has been defined, either by the user or a random one,
the user can click cities in succession to trace the route to follow.
Clicking a point already added to the path will remove all tracks back to
that point. (Handy if you find that you missed a city.) User and
program paths can now be saved in a text file for printing or future
reference.
February 25, 2017: A programmer
trying to convert Latitude/Longitude coordinates to points on a Mercator
projection recently wrote asking for help. This program was the logical
example for him, but it would not compile with Delphi versions after Delphi 7.
Version 3.1 posted this week uses compiler directives to determine Delphi
version and generate code which should compile under old or new Delphi versions. As
usual when a program is revisited, text errors were corrected and forms layout
and displays improved over the previous version.
Running/Exploring the Program
Suggestions for Further Explorations
 |
Sept 7, 2011 Done! Allow user to retract selection while drawing the path.; |
 |
June 20, 2002 Done! It just
occurred to me that when doing exhaustive searches for round trip
routes, half of the arrangements are reversed versions that needn't
be checked. For example, if we have checked path [1,2,3,4] we
don't need to check path [4,3,2,1] because the distance will
be the same. Come to think of it, we also wouldn't need to
check rotations [2,3,4,1], [3,4,1,2], [4,1,2,3],
[3,2,1,4], [2,1,4,3], or [1,4,3,2]. Eliminating 7 of
every 8 permutations could speed things up considerably.
Hey! Even better - isn't it the case that after we check the
permutations that begin with city # 1, we have checked all of the
unique routes and can stop. If the user un-checks that "Roundtrip" box, it's a different
story.
This change reduced exhaustive search time for shortest 13 city closed
route from 3 hrs 26 min to less than 12 minutes - just
too good to resist. |
 |
Fix
"Branch and Bound" heuristic code. |
 |
More sophisticated heuristics. |
 |
Current
sophisticated techniques produce solutions that are said to be known to be optimum.
They obviously don't determine this by checking all possible paths.
So, as my brother once asked about thermos bottles that keep
hot things hot and cold things cold, "How do they know?" |
 |
There is untested code in the program
which should allow other maps to be loaded (of a single state
or another country, for example), so long as a comparable cities
file is also provided. I'll get around to testing at
least a single state version one of these days. |
 |
There is also disabled code to allow
user to maintain the "Cities list" file by using a separate dialog
to define additional city names and locations from within the
program |
| Original Date: June 17, 2002 |
Modified:
May 15, 2018
|
|
|

