A simulation program for an aircraft instrument simulator called the Horizontal Situation Indicator is under development here at DFF.   This Wind Triangle program was written to make sure that I understood the concepts and mathematics for navigating an aircraft in the desired direction.      

Objects moving though still air generally move in the direction they are pointed. However moving air, i.e. the wind, will alter the course and speed of the object relative to the ground depending on the wind direction and speed.

Correcting for the wind is a necessary skill for airplane pilots, expert marksmen, and successful golfers. Only airplanes generally fly slow enough and high enough that mathematically calculating the wind correction angle is worthwhile. The technique uses "vector addition". Vectors are line segments that have a specific direction, i.e. they are defined by a length and an angle. In our Wind Triangle we'll have three vectors:

• The Wind vector defined by Wind Direction and Windspeed.  
• The Heading vector defined by the Heading Angle and Airspeed. This is the path that the plane would take in still air.
• The Track or Course vector defined by the Course Angle and speed (Groundspeed) of the plane over the ground.  It's the result of the Wind vector acting on the Heading vector.

Note that speeds substitute for distances here which is OK since they are directly proportional.  Under constant input conditions, whether you fly for one minute or one hour, the distances traveled will be in proportion to the speeds  and the triangle will have exactly this same shape whichever variable is plotted.    

WTA=Wind to track Angle WCA= Wind Correction Angle

In most cases, we want the Course to be an input and calculate the proper heading into the wind to offset its effect.  Search the web for "Plot Wind Triangle" and you will find a number of pages describing the geometric construction technique.

This program  provides an interactive version that uses trigonometry to determine the Heading that will keep us on the desired Course. Playing with it will help develop an understanding of how the variables interact. A summary of the equations used is given for each output.

: 

The Equations

 We are given 4 values as input.  (Wind direction, Wind speed,  Airspeed and Desired Course Angle).   This is the minimum required to define the triangle and orient it in relative to North.   Here are the essential equations used to calculate the missing parameters for our Wind Triangle: .  

Wind Direction Adjustment

WindDir = Input WindDirection +180° 

Since Wind directions are given as "From" direction rather than "To", we'll add 180 degrees to get our vector point in the correct  (downwind) direction..

Wind To Track Angle:

WTAngle =  DesiredCourse - WindDir 

The input angles Wind direction (WinDir) and Desired Course (DesiredCourse) are fixed angles independent of any other values.  The difference is calculated as a convenience  in references in the equations below.

Wind Correction Angle

SinWca:=windspeed*sin(WTAngle)/Airspeed; 
WCA:=arcSin(sinwca); 

We'll define the Wind Correction Angle (WCA) to be the angle that our Heading Angle  must deviate from the DesiredCourse to correct for the effect the the Wind is having on our aircraft.  

The Sine Rule in trigonometry  says that  lengths of the sides of a triangle are in the same proportion as the sine of the angles opposite those sides.  I.e. If one side is twice as long as another, the sine of the angle opposite the longer side will be twice as large as the sine of the angle opposite the shorter side. For our triangle this implies that : Sin(wca)/windspeed = sin(WTAngle)/airspeed which leads to the above equation .

Heading

Heading:=DesiredCourse+WCA;

By definition the Wind Correction Angle is the angle between the Heading and the Desired Course:  WCA = Heading - DesiredCourse  which leads directly to the above equation.

Groundspeed

groundspeed = airspeed*cos(WCA) + windspeed*cos(WTAngle)

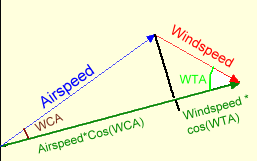
We'll use the definition of Cosine (Cosine=adjacent side/hypotenuse) to calculate the length of the groundspeed vector.  By dropping an altitude from the vertex opposite the course side, we can divide our Wind triangle into two right triangles as shown here.   The sum of the two adjacent pieces is the groundspeed. 

We  also have enough information to use the Sine Rule or the Cosine Rule to calculate groundspeed.  All three methods produce the same answer,  but the equation used here is slightly less cumbersome.  

Addendum: October 13, 2006:   Since publishing the Wind Triangle program in February, 2005,  I have had several pilots inquire about implementing an Excel spreadsheet version.   The typical problem they had was not realizing that the trig functions require  angles to be specified in radians instead of degrees.   (Also true in Delphi and most other languages.)  Patrick C. recently sent his "Flight Planning Worksheet"  Excel file and I  fixed his calculation for True Heading and Ground Speed..  With his kind permission, I decided to make it available for downloading as a prototype for the  next pilot  working on the problem.     Patrick lives (and flies a Cessab 172) in new Zealand.  They measure fuel in liters and, at least in his spreadsheet, distance and speed in nautical miles and knots.   The fuel, speed, and distance calculations would not change for  other measurement systems. 

Running/Exploring the Program 

Download source code

Download executable 

Download Excel Flight Planning Worksheet