Problem Description
Write a program to investigate the math
behind to circles which intersect, specifically the points of
intersection .
Background & Techniques
This problem came to mind while was
writing demo code to draw the Olympic rings and needed to redraw
small arcs around the points where the rings intersect to give
illusion of one ring passing over or under another. It
turns out that redrawing by quadrant was good enough for that
application, but the problem of determining exact points of
intersection sounded, and has been,
interesting. A good review of your high school
trigonometry if nothing else.
The code for this program is based
on a description by Paul Bourke and C code by Tim Voght found at http://astronomy.swin.edu.au/~pbourke/geometry/2circle/.
All I added was the conversion of the code to Delphi, a
test program and an
expanded explanation of the math involved.
Mr. Bourke made several leaps that were not obvious to
me, but after several hours of enjoyable study, I think I
understand it.
I modified Paul’s diagram with a
few extra labels like this:
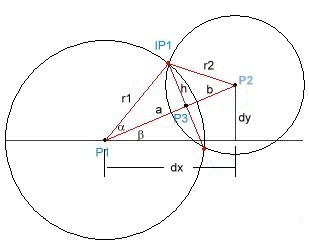
P1 and P2 are
circle centers located at (x1,y1) and (x2,y2).
dx and dy are the x and y offsets of
P2 from P1.
dx
= x2-x1
dy = y2-y1
Pythagoras tells us that the
distance between P1 and P2 is d =
sqrt(dx*dx+dy*dy).
If d
is less than then sum of the radii of the circles, r1+r2,
then the circles may intersect. (There is still the chance that P2 is
so close to P1 that it is entirely contained within
and still does not intersect.
This is true if and only d<|r1-r2|
. Imagine that
the circles a concentric, share the same center.
Then the distance from the rim of the inner circle to the
outer is the absolute value of the difference in radii.
If d becomes greater than this distance the
circles again intersect until it exceeds the sum of the radii.)
Assuming the circles intersect, we want to find the
coordinates of the points or points of intersection, IP1
and IP2. ( For
clarity, I left the label off of IP2
on the diagram above).
So
we have enough information given to solve for a and h.
Considering the right triangle IP1P1P3,
we can write cos(a)= a/r1
where a is the angle
at P1 .
Also
by considering triangle P1P2IP1
, we can apply the "Cosine law" to get another
expression for cos(a).
Law
of Cosines: Cos(a)=(r12+d2-r22)/(2r1d)
Therefore
cos(a)= a/r1= (r12+d2-r22)/(2r1d)
and multiplying both sides by r1 leaves
a= (r12
- r22 + d2 ) / (2 d)
If the circles touch at one point,
you can substitute d=r1+r2 in the
above equation and prove that a=r1 at the
single point of intersection.
Once we know a, we can find
the value for h as h=sqrt(r12 -
a2).
Whew, just one more critical step
to find the actual coordinates of the intersection
points The trick here is to conceptually
rotate point P3 down so that it lies on the
x-axis. We don't know what that angle is yet, but we'll
call it, -beta, -b.
Then the coordinates of P3 relative to P1
would be (a, h). Now if we rotate
through the point (a, h) back up by angle b,
it will be at the upper intersection point.
The other point if it exists, will be the result of rotating the
point (a, -h).
So if we look up 2D rotation equations (at this
site , for example, we'll find the equations for rotating at
point through a given angle.
x' = x cos b - y
sin b
y' = y cos b + x sin b
To apply the rotation up by b,
we need its value, or at least the values for sin( b)
and cos(b).
These are defined by the triangle formed by sides d, dx
and dy in the above diagram so Sin(b)
= dy/d and Cos(b) = dx/d.
One final consideration, since the above equations assume
that we are rotating about the origin( (0,0) and we are actually
rotating about P1 at (x1,y1),
we need to translate the final coordinates back by adding (x1,y1)
to the rotated values. .
Our intersection points are therefore: IP1.x
= x1 + a*dx/d - h*dy/d and IP1.y
= y1 + h*dx/d + a*dy/d
or
IP1.x = x1 + (a*dx -
h*dy)/d and , IP1.y = y1
+ (h*dx+a*dy)/d
and for the lower intersection (a,-h)
rotated by b,
IP2.x = x1 +
(a*dx + h*dy)/d and IP2.y =
y1 + (-h*dx+a*dy)/d
As they say in Latin. "Q.E.D.", which loosely
translates as "We have arrived at our destination" .
I'll skip coding notes on this one - not much special and the
math description wore me out!
Running/Exploring the Program
