What's New - January 2016
[Home]
January 1, 2016:
Happy New Year to all!
January 2, 2016:
 OK,
holidays are over; back on the diet and back to "work" programming. Being
known to the family as a puzzle lover, I received one called "Aristotle's Number
Puzzle" for Christmas this year - nothing to do with Aristotle as far as I can
tell. It's a hexagon shaped board made up of of 19 hexagon shaped tiles numbered
1 through 19. The objective is to arrange them into a "magic" hexagon in
which values in every horizontal and diagonal row (15 in all) sum to 38.
Our "Brute Force" program can
find the 12 variations of the solution by defining 15 equations representing
sums for the 19 variables . These are all isomorphic versions of the single
solution, i.e. they represent rotations and mirroring of the solution. I decided
to investigate further, starting by posting a Delphi Techniques program to draw
Hexagonal Boards of
various sizes. Here's one with puzzle hints filled in.
OK,
holidays are over; back on the diet and back to "work" programming. Being
known to the family as a puzzle lover, I received one called "Aristotle's Number
Puzzle" for Christmas this year - nothing to do with Aristotle as far as I can
tell. It's a hexagon shaped board made up of of 19 hexagon shaped tiles numbered
1 through 19. The objective is to arrange them into a "magic" hexagon in
which values in every horizontal and diagonal row (15 in all) sum to 38.
Our "Brute Force" program can
find the 12 variations of the solution by defining 15 equations representing
sums for the 19 variables . These are all isomorphic versions of the single
solution, i.e. they represent rotations and mirroring of the solution. I decided
to investigate further, starting by posting a Delphi Techniques program to draw
Hexagonal Boards of
various sizes. Here's one with puzzle hints filled in.
January 20, 2016:
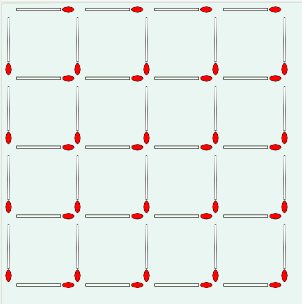
There are 30 squares of all sizes in a 4x4 grid of 40 matchsticks. "What is the minimum number of matchsticks that need to be removed to leave no squares of any size?"
How many Squares? investigates this problem, from the latest addition to my library of math & puzzle books: Challenging Math Problems, Terry Stickels, Dover Publications, 2015.
Program users can investigate various grid sizes and work on solving by
clicking to add or remove matchsticks with feedback along the way.
For those with a little mathematical curiosity, there are some interesting
relationships across grid sizes among the number of matchsticks, the number of
squares, and the minimum number of sticks to eliminate .
January 28, 2016: It did not take long to recognize
the need for for the first two enhancement suggestions in last week's HowManySquares program.
HowManySquares Version 2 adds the ability to view remaining squares after
each move or on request. Also grids can now be saved and restored.
Both features are helpful when working on larger grids. So far I've solved
(and saved) up 7x7 grids. Still working on 8x8.
