What's New - August, 2008
[Home]
August 27, 2008: While updating the game of HIP last week, I ran across a note about a suggested rules variation that would make the game more interesting. In the original game, with players A and B alternating moves, player B has a large advantage because he can often play symmetrically opposite to A's move and guarantee that A will complete a square first and lose. In the variation, posted as HIP Version 4, each player, after the initial move by player A, must select two points and still avoid forming a square. It appears to make the game, especially the 6x6 version, much more fair.
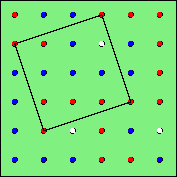 |
|
Red loses! |
August 22, 2008: Viewer Sadanand wrote recently challenging a statement I had made about there being only one tie game for the 6x6 version of Martin Gardner's game of "HIP". (First to form a square loses, and "squares" are not "Hip")
Actually the statement was Gardner's and he later modified to "essentially" only one tie game based on additional feedback to his Scientific American column which introduced the the game. The game appears in his Dover book My Best Mathematical and Logical Puzzles available from Amazon.
Sadanand found three additional tie games, one of which
matched Gardner's by rotating and reversing colors. The others cannot
be so transformed. We settled on three essentially different tie games.
HIP Version 3 replays the three
tie games as well as adding 5x5 and 7x7 game sizes and the ability to
retract moves.
August 19, 2008: A couple of updates this week:
Our CuttingStock application designs a strategy to minimize costs for cutting parts of specified lengths from stock of specified lengths. CutStock Version 3 sorts the input parts list by input part length before solving and improves the graphics rod display when a large number of short parts are cut from long stock. These changes allowed a solution to be found for a user submitted case with a large number of different part lengths (19) and wide range of part lengths (134 to 6004).
ReactionStats Version 2 adds some Student's T-Test statistics to the output display along with more text explaining the results. This program analyzes results from our reaction time measuring program. I'm excited because a biology instructor at a community college is interested in using the program to introduce students to statistical analysis of sample data. What a novel approach! I'll be supporting in any way I can to help her get the concepts across. The attached sample data file used for testing indicates that my mean response times have increased by 0.03 seconds in the last 4 years. Worse, there is a 95% chance that the difference is significant and that I am indeed slowing down! I was hoping that it was just my imaginationJ.
August 11, 2008: The Delphi StringGrid control is handy for displaying table data and game boards on the screen. Unfortunately, printing them is either easy but not very flexible (Form Print procedure) or flexible but not very easy (my PrintPreview unit), depending on the method chosen. Today's posting, PrintGridTest in the Delphi techniques section of DFF introduces PrintGrid procedure that is somewhere in between.
August 6, 2008: DelphiForFun Newsletter #50 was sent yesterday; a milestone of sorts I suppose. Actually, it was sent twice because the first try had broken links. Publishing a quarterly newsletter allows just enough time to forget how to reliably keep track of links and graphics as items are copied and assembled. The newsletter is mainly a compilation of the "What's New" items for those who may not visit DFF regularly but would like the occasional chance to scan postings for items of interest.
Changed versions of our Intersecting Lines test program and the two intersection testing functions were posted today. The final versions I hope. It successfully compares millions of randomly generated pairs of lines using the two intersection testing functions. An interesting question was raised by this testing: "What is the probability that two randomly generated lines within given rectangle will intersect?" Testing a million pairs at a time, the empirical answer is about 0.231. If anyone derives of knows of the analytical answer, let me know.
August 3, 2008: Intersecting Lines is a program to test a LinesIntersect function which returns a "true" or "false" condition based on whether two given line cross each other. Changes were posted today to correct a rare error condition where non-intersecting lines were reported as intersecting. Library file DFFLibV11 which contains the UGeometry unit which contains the LinesIntersect function was also reposted. Another example where my 4 year old grandson can beat my complex algebra based program in deciding whether two lines touch or cross each other! How do we do it?
