

[Home] [Puzzles & Projects] [Delphi Techniques] [Math topics] [Library] [Utilities]
|
[Home] [Puzzles & Projects] [Delphi Techniques] [Math topics] [Library] [Utilities]
|
|
Problem Description
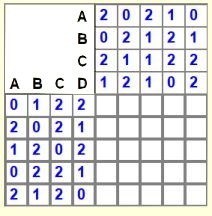
Place one of A, B, C, D into each of the 25 empty cells so that the number of letters in each row and column areas is as indicated by the numbers. Identical letters cannot be next to each other in the grid either horizontally or vertically.
|
| Validates that the key can be placed without violating the "no adjacent duplicates" rule | |
| Creates the Pathlist entry and appends it to the list. | |
| Decrements the character count column and row fields for this cell, and | |
| Enters the keyed character in the selected cell. | |
| Checks if all 40 count cells have '0' value and shows a Contratulations" message if so. |
The "Undo" button required keeping track of the previous character as letters are entered. A "PathList" stringlist does this with 2 character keys; the new character end the replaced character. A simple TPathObj object in each list entry contains the column and row information required when multiple "Undos" are requested.
The auto-solve section of the project was a logical candidate for some sort of exhaustive search with backtracking. However , with 4 letter choices for each of the 25 cells to fill, the upper limit of tests is 425 (420 if we exclude the 4 adjacent cells which cannot contain the same letter), That smaller number is still more than a trillion tests and led me to the "solve by column" strategy. The algorithm first checks for any count of 3 letters in a row or column. The 3 Bs in row 5 allows to fill cells [4,5] [6,5], and [8,5] with Bs immediately. Similarly, the 2 Bs specified for row 6 must be placed in [5,6] ad [7,6]. So we now have only 4 letters to place in each column. The bad news is that we must also now keep track of which 4 rows need to be filled. I used an "Indices" array to hold the locations built by examining the rows in the current column and entering those with blanks into the Indices array. The required number of occurrences of each of letter must match the number or of blanks found in the column they will allows us to build and initial "PermutedLetters" array.
The Combos class will let us generate all permutations of the required letters and one of them must be correct if a solution exists. The recursive FillNext function does the grunt work for each column. Because of the recursive nature, we need an array of Combos controls, one for each column. Here's an outline of the jobs performed:
| Building the Indices array giving the rows where the letter will be place. | |
| Building the PermutedLetters string | |
| Generating and validating each permutation to ensure both the "no duplicate neighbors", and positive available letter counts for the cell column and row. | |
| Duplicate letters in ithe PermutedLetters will produce duplicate permutations so the first occurrence of each set will be saved in the "TryList" stringllist and further duplicates are skipped if already in the list. Again, because of the recursion activity, we need a unique Trylist for each column, so we actually have an array of these lists. | |
| When a column has been successfully placed, FillNext calls itself passing the next column number if there are more columns fill. If the last column has been filled, we have a solution and the user is given the choice of stopping or continuing the search. If the function call returns a False Result, we continue in the loop generating the next permutation. If we run out of permutations without a True Result, we pass False result back to the guy that called us (the previous column loop), so he can do the same thing. |
That's a brief summary of all that happens in finding a solution. The code is semi-generalized to handle other puzzle sizes, but since none are known to me, I have depended on four letter choices in a 5x5 array in some of the code I'm sure. That will leave something to work on when the time comesJ.
September 22, 2017: Finally a 2nd puzzle of this type
showed up in our Mensa Puzzle calendar (September 7th, at right).
Version 2 of MindYourABCDs corrects some typos in the original and allows player
to choose which puzzle to tackle.
| Download executable | |
| Download source (Note: Program uses the CombosV2 and DFFUtils units which reside in our library zip file of commonly used units. Library file DFFVLIB13 or later is required to recompile this program ) | |
| Download
current DFF
Library file [DFFLibV15]
|
|
|
Generate new random puzzles. (Generating should be easy, generating puzzles with a only one solution might be harder.) |
|
|
. |
|
|
| Original: August 28, 2016 |
Modified: May 15, 2018 |
[Feedback] [Newsletters (subscribe/view)] [About me]Copyright © 2000-2018, Gary Darby All rights reserved. |