
Search

As of October, 2016, Embarcadero is offering a free release
of Delphi (Delphi
10.1 Berlin Starter Edition ). There
are a few restrictions, but it is a welcome step toward making
more programmers aware of the joys of Delphi. They do say
"Offer may be withdrawn at any time", so don't delay if you want
to check it out. Please use the
feedback link to let
me know if the link stops working.

Support DFF - Shop
If you shop at Amazon anyway, consider
using this link.
We receive a few cents from each
purchase. Thanks

Support DFF - Donate
If you benefit from the website, in terms of
knowledge, entertainment value, or something otherwise useful,
consider making a donation via PayPal to help defray the
costs. (No PayPal account necessary to donate via credit
card.) Transaction is secure.

Mensa®
Daily Puzzlers
For over 15 years
Mensa Page-A-Day calendars have provided several puzzles a year
for my programming pleasure. Coding "solvers" is most fun,
but many programs also allow user solving, convenient for "fill
in the blanks" type. Below are Amazon links to the
two most recent years.
Mensa®
365 Puzzlers Calendar 2017
Mensa®
365 Puzzlers Calendar 2018

(Hint: If you can
wait, current year calendars are usually on sale in January.)

Contact
Feedback:
Send an
e-mail with your comments about this program (or anything else).

|
| |
Problem Description
Variation of Puzzle #383 from H. E. Dudeney - Amusements in Mathematics, Dover Publications
Select the Ace through 9 of any suit from a deck of cards and arrange them in a 5X5 T shape like this:
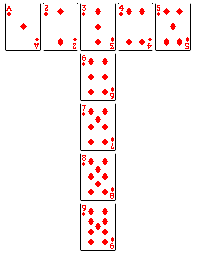 Notice that the sum of the digits in the crossbar
(1+2+3+4+5=15) is not the same as the sum of the cards in the upright
(3+6+7+8+9=33). But by rearranging the cards, the sums can be made
equal. In fact this may be accomplished in 18 distinct ways. How many unique solutions
can you find? Notice that the sum of the digits in the crossbar
(1+2+3+4+5=15) is not the same as the sum of the cards in the upright
(3+6+7+8+9=33). But by rearranging the cards, the sums can be made
equal. In fact this may be accomplished in 18 distinct ways. How many unique solutions
can you find?
"Unique" in this version means that the
same 5 numbers may not be repeated in any order in the crossbar nor in the
upright. Also merely exchanging a solution's upright and crossbar will
not produce a new solution. Dudeney's original version counted each
permutation of the digits as unique resulting in more than 10,000 solutions! So
finding only 18 should not be too hard.
A little analysis will convince you that the card at
the intersection of the crossbar and upright must be odd. The sum of
the crossbar and upright cards are equal so the sum of all 10 cards,
(including
the intersecting card twice), must be divisible by 2, i.e. even. Since the sum of the 9 cards
is odd, the extra intersecting card value must also be odd to make the total come
even.
Background & Techniques
Non-programmers are welcome to read on, but may want
to skip to the bottom of this page to download an executable version of the program.
For programmers. there is nothing too complex
here. Using the tried and true "divide and conquer" problem solving
technique, the main sub-problems are :
 | Define a data structure and procedures to keep
track of and check solutions. |
 | Creating, placing dragging the cards. |
 | Finding all solutions programmatically so we can
display them on request. |
 | The usual user interface design decisions. |
Data Structure
I chose a stringlist to hold solutions. The strings are 5 characters
in length arranged with the intersecting card value first followed by
the other 4 values in the crossbar or upright arranged in ascending
order. This guarantees that each 5 digit string represents a
unique solution. Since this may represent either the sum of
upright or crossbar values, we need to check both possible keys when we check
a particular arrangement. Checking for
solutions actually occurs in three places in the program.
Function UpdateSums does a preliminary check as it updates the
labels which display the current crossbar and upright sums and returns true
if the sums are equal. Function IsNewSolution returns true if
the sums are equal, that the center card is odd and the solution
is not already in the the SolutionList Stringlist. And
procedure ComputeSolutions is called from FormCreate to compute all 18
solutions initially and place them in the AllSolutions
Stringlist.
Card Handling
The 9 cards are held in an array of TCard objects created by the U-CardComponent
unit. A CardSlots array contains 9 TSlot
records defining the upper left corner of the cards in the T and the
addresses of the cards currently occupying each slot (or nil if the
slot is unoccupied). The cards are created dynamically and have
pointers to the mouse handling routines (OnMouseDown, OnMouseMove,
and OnMouseUp). As usual in dragging operations, OnMouseDown
sets a flag indicating that the card is being dragged. We also
determine if the card is in slot and save this FromSlot number so
we can swap cards when the OnMouseUp occurs (if it is dropped on an occupied
slot in the T). The original version did not swap,
but required that a card be off of the T to empty a slot before a card could
be dropped there. It turns out that (except for the intersecting card
position) the order of cards within the T is not significant and
swapping cards is a perfectly adequate way to generate new trial
solutions. Removing the extra code required to support
dropping cards off of the T, moving them back, checking that the T is
full, etc., is left as an exercise for the
viewer.
The OnMouseMove exit mainly updates the left and top
coordinates of the card being dragged. I move the cursor to the
center of the card being dragged at mouse down time so OnMouseMove has to back up half
the card width and half the card height to set the top left card corner
coordinates based on the current mouse position. OnMouseUp
has quite a bit of work to do checking whether the dropped position is on a
card slot, represents a solution, and further, a new solution.
Finding All Solutions
At startup time, procedure ComputeSolutions is called to initialize
a list, AllSolutions, of all solutions. The list is used to assign a solution number
(simply its position in the AllSolutions list) when the user find a
solution and to find the solution to display when the user clicks the "Show
Solution #" button. Our old friend, the TComboSet class
defined in the Combos unit, is used to generate all combinations of 4
cards selected from 9. Each combination is assumed to be 4 cards
of an upright or crossbar excluding the intersecting card. We must
combine each of these sets with each possible intersecting card not
already in the 4 selected to see if they form a solution. ComputeSolutions
was written before the IsNewSolution function. It could probably
be shortened by calling a slightly modified version of IsNewSolution,
but I didn't bother. Maybe another exercise for the viewer.
Interface Design
I try to make programs fit into a 640x480 screen size out of consideration
for viewers with older equipment. . This is one of the few programs
where I could not. I am also not really satisfied with the
method for indicating to the user which of the 18 solutions he has found so
far. I wanted 18 little boxes that somehow would show the configuration
of each solution as it was found. I never quite made it there
- the compromise uses a stringgrid to show counts of total solutions
and solutions found for each of the 5 possible intersection
cards. I guess its OK - if you don't like it, write something
better yourself!
There is a toot.wav file included with the program which plays a
short train whistle effect when new solutions are found - just for fun!
Note for future reference: I used the AdjustGridSize procedure
make the scoring stringgrid just big enough to contain the cells. I
discovered this time that the resizing leaves extra room for scroll bars unless
the Scrollbars property is set to ssNone.
Running/Exploring the Program
Suggestions for Further Explorations
 |
Dudeney has many other card arrangement problems in
the referenced text. |
 |
It
seems like there should be a neat analytical way to prove that there at
most, at least, or exactly, 18 solutions, but I couldn't find
it. Can you? |
 |
Several
possible enhancements were described in the write-up above - if you
want to try your hand. |
| Original Date: December 16, 2002 |
Modified: May 15, 2018
|
|
|

