
Search

As of October, 2016, Embarcadero is offering a free release
of Delphi (Delphi
10.1 Berlin Starter Edition ). There
are a few restrictions, but it is a welcome step toward making
more programmers aware of the joys of Delphi. They do say
"Offer may be withdrawn at any time", so don't delay if you want
to check it out. Please use the
feedback link to let
me know if the link stops working.

Support DFF - Shop
If you shop at Amazon anyway, consider
using this link.
We receive a few cents from each
purchase. Thanks

Support DFF - Donate
If you benefit from the website, in terms of
knowledge, entertainment value, or something otherwise useful,
consider making a donation via PayPal to help defray the
costs. (No PayPal account necessary to donate via credit
card.) Transaction is secure.

Mensa®
Daily Puzzlers
For over 15 years
Mensa Page-A-Day calendars have provided several puzzles a year
for my programming pleasure. Coding "solvers" is most fun,
but many programs also allow user solving, convenient for "fill
in the blanks" type. Below are Amazon links to the
two most recent years.
Mensa®
365 Puzzlers Calendar 2017
Mensa®
365 Puzzlers Calendar 2018

(Hint: If you can
wait, current year calendars are usually on sale in January.)

Contact
Feedback:
Send an
e-mail with your comments about this program (or anything else).

|
| |
Problem Description
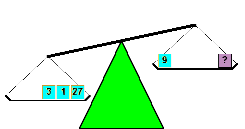 Once some kids wanted to set up a lemonade stand to make
money. To set themselves apart from the other lemonade stands on the block, they decided to sell their lemonade by the pound. They found an old balance beam scale, the kind with a weight pan on each side, and three weights. They discovered that they could sell any whole number of pounds from 1 to 13. What weights did they have.? Once some kids wanted to set up a lemonade stand to make
money. To set themselves apart from the other lemonade stands on the block, they decided to sell their lemonade by the pound. They found an old balance beam scale, the kind with a weight pan on each side, and three weights. They discovered that they could sell any whole number of pounds from 1 to 13. What weights did they have.?
Background & Techniques
This program was motivated by an email I sent
recently to my
13 year old granddaughter at camp. (Email at
camp? What a different would we live in today!)
She happened also to be in cabin 13 so in
addition to the lemonade problem, I included a few facts about the number 13
designed to help overcome triskaidekaphobia.
e.g.
 | 13 is the smallest "emirp", a prime that forms a different prime when its digits are reversed. I wonder what the second smallest is. |
 | Unless I'm mistaken, ELEVEN + TWO anagrams to TWELVE + ONE |
 | The longest recorded flight of a chicken is 13 seconds. |
 | Of course 13 is also a Fibonacci number, so you can check local pine cones for 13 spirals in the seed pattern |
The lemonade weighing problem is not too difficult to solve by trial and
error, but it aroused my curiosity about weight sets with 2, 4, 5, or
more weights. How many values can be weighed by each of those
sets? How can we determine the optimum values for the
weights?.
There are actually two programs here - the main form searches for the best
set of weights for a user specified number of weights from 1 through
5. "Best" means capable of weighing any unknown item
with integral weights between one and the sum of all the
weights. A "Play with the scale" button on the
main form displays a screen with a simple animation of a balance beam scale
and unknown weights that you can "weigh" by placing the known
weights on the balance pans with the unknown item.
After the program was written I found that there are simple analytical
solutions that confirm the program results, but it was an interesting mental
exercise anyway. Here's a link to an good analytical
treatment by Spyros Potamianos from newsgroup rec.puzzles and archived by
Arlet at rec-puzzles.org.
I'm not sure who Arlet is, all I could find at the site was a picture of this
kind of ugly guy, but he is doing a good job of preserving the contents of an
interesting newsgroup. Search on "optimal
weights" to locate the article by Spyros.
Non-programmers are welcome to read on, but may want
to skip to the bottom of this page to download an
executable version of the program.
Notes for Programmers
The search procedure is a little bit complex and any description would
probably sound like a journal paper; so for the one or two people who might be
interested, I've tried to put good comments in the program. If you
want to know and can't figure it out, send me an email.
The second part, the animated scale, is easier. A TScale
object was defined as a descendent of TImage to contain the scale
image and information about the weights on each pan. Drawing is
done on Tscale's Canvas with separate methods for drawing
 | the base, DrawBase; |
 | the beam which sets on top of the base and tilts 12 degrees left of
right depending on which side is heavier DrawBeam; and |
 | the pans, one suspended from each end of the beam and which visually
holds the weights, DrawPans. |
Procedure DrawScale calls each of the above routines in
succession specifying the new angle of the beam. Drawing is performed
10 times in a loop, moving 1/10 of the total rotation angle each time
through.
Keeping track of the weights was made a little trickier by my decision to
place the unknown weight on the outside of its pan and known weights on the
inside. This made it necessary to keep track of the unknown weight
separately from the TList structures, LeftWeights and RightWeights,
which are used to keep track of the known weights.
The weights are TStaticText objects just because they seemed the
simplest controls that allowed internal text to be aligned and could be
colored. Since they will be dragged onto of off of the scale,
they remain parented by the form. Detecting when weights
were removed was a particular problem. OnStartDrag exits for the
weights weren't always triggered for some reason. I solved the problem
by always attempting to remove a weight when it was dropped on the scale (to
handle the case of a drag from a pan to a pan). An OnDragDropExit
for the Form detects the case where a weight was removed from a pan back to
the form area outside the scale image.
A few other items that might be on interest:
 | TScale uses a callback procedure (OnBalanced) to notify
the form when the scale is in balance. The definition for a
procedure type that is a method (mine is), mist include the phrase
"of object" . So the definition is Onbalanced:
Procedure of object; |
 | TLists are an excellent way to keep track of objects - remember that
object references are actually pointers to the objects, so space usage is
minimal and detecting whether a particular object is in the list (i.e. in
the weight pan) is a simple matter. |
 | Drag/drop processing basically requires three steps:
 | change Dragmode from dmManual to dmAutomatic in
the object to be dragged. |
 | define a OnDragOver exit for any control where the object may be
dropped. Set the passed variable Accept to true in this exit.
The object being dropped is passed in variable Source, so you
can check if necessary to make sure that you want to accept
it. |
 | define an OnDragDrop exit to process the logic when the object
is actually dropped. Again the object being dropped is passed in
variable Source so in our.Scale dragdrop exit we can update
it position to move it to the closest weight pan, and we can add to
to our list of weights in this pan. |
|
 | In generating a random weight, I decided to also generate a random
color. There is a Windows SDK function RGB for this, but I
noticed a significant delay when using it. My equivalent used
here is unknownweight.color:=(64+random(192)) shl 16+ (64+random(192)) shl 8 + (64+random(192));
This sets each of the low order bytes of unknownweight.color to a
random number between 64 and 255. The lower limit of 64 eliminates
very dark colors. The shift left (shl) instructions could
be replaced with multiply by 256 (shl 8) and 65538 (shl
16). Delphi is smart enough to use shl to multiply by
powers powers of 2. |
OK, let's get on with it!
Running/Exploring the Program
Suggestions for Further Explorations
 |
There's a
great On-Line
Encyclopedia of Integer Sequences sponsored by AT&T. Our
sequence, for the maximum weighable item for N known weights, searchable
from the index page, is
number A003462.
You can learn more about it there, and get sidetracked to many other
sequences in the process. |
 |
Also
the rec-puzzles.org
archive link will
provide many hours of happy browsing. |
 |
The other
frequently encountered weighing problem is the Counterfeit weight
problem. Given N coins with one of them counterfeit, and a balance
beam scale, what is the minimum number of weighing necessary to find
the bad coin? In different variations we may know that the
weight of the counterfeit is light, heavy, or just
different. The scale in this program could provide a
starting point for
a program handling problems of this type. |
| Original Date: July 20, 2002 |
Modified: May 15, 2018
|
|
|
|

