Problem Description
Here's a program which displays the
shadow cast when sun is at a given azimuth and altitude.
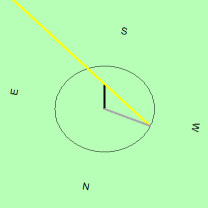
Background & Techniques
Based on a user's request, here's an attempt to
draw a 3D image of the shadow of a vertical rod produced by the sun at a
given azimuth and altitude.
A second set of edit controls allow you to change
your viewpoint by adjusting the bearing, altitude, and distance from the
base of the rod.
A late addition was the ability to plot an "analemma", a figure representing
the path of the sun af observed from a fixed location and time of day for an
entire year. Because the earth is tilted relative to is path around the sun
and because it's path is slightly elliptical, the analemma, or its shadow
version, traces a lopsided figure 8. Azimuth and altitude points may be
entered individually and the "Plot shadow point" button clicked. A better
method is to build a text file of azimuth and altitude values, one pair per
line, and use he "Load Analemma" button to load and plot the data. File
"Sample Analemma.txt", included with the downloads, has 24 values for
noon on the 1st and 15th of each month for my home town.
Non-programmers are welcome to read on, but may
want to skip to the bottom of this page to download
executable version of the program.
Notes for programmers
I wish I could give you a concise analysis of the math behind drawing a
3D shadow view, but the fact is, there was a lot of trial and error to draw
the images. There are six parameters altogether: Azimuth and altitude
define the direction of the sun from a particular location on the earth's
surface the "Horizontal Coordinate System". Azimuth is the angle
clockwise from North and Altitude is the angle above the horizon.
The third parameter affecting the true position of the tip of a vertical
rod's (or person's) shadow is the height of the rod. For a give
altitude and rod height (R), the length of the shadow (L) can be
derived from considering the right triangle formed by the rod, its shadow
and the sun ray. Tangent(altitude) = R/L, from which we can define
the circle with radius L upon which the shadow tip will lie. The azimuth angle
determines exactly where on the circle the point lies. Procedure
RecalcBaseCircle does this every time one of the three position
parameters changes.
The base circle represents the shadow tip points as we would see them
when standing directly over the rod looking straight down. When
we move away from the rod in a given direction for a given distance with our
eye at a given height, the apparent position of the shadow changes.
These three "Eye" parameters determine the apparent location of the shadow
tip on an ellipse. This set of points is calculated by the
RecalcVisualCircle procedure. It is called whenever the eye
position is changed or when the base circle changes.
The third set of trigonometric calculations came from my, perhaps
foolish, decision to display directional letters N, E, W, S
representing our eye position bearing (direction) from the rod. Since we cannot
actually rotate the monitor screen as we walk around the rod, we must rotate
the view circle and those letters on the screen. In order to make the
letters appear as if they were painted on the ground, I decided to rotate
them as they moved in a circle concentric with the view circle so that the
base of the letter was always facing the rod. This is
performed by the SetFontAngle procedure. The code to draw
the letters is contained in the PaintFigure procedure which redraws
the entire image. It looks like this sample for the letter N
(North):
sing:=sin(eyeAlt);
angle:= (eyeaz-halfpi);
sina:=sin(angle);
cosa:=cos(angle);
setfontangle(font, -angle+halfpi);
x:=midx-trunc(letterdist*cosa);
y:=midy-trunc(letterdist*sina*sing);
textout(x,y,'N');
And finally, I decided to allow shadow points to be saved and plotted
each time the image is redrawn This introduced its own set of problems
since the points have no relation to the current base circle .
Whew! For the first forty hours working on a
program, it's great fun. After the 2nd forty hours, one is ready for the
darn thing to just work! That's about where this program lies now and I'm movin' on. But I'm already looking forward to doing it all over
again with a new project next week!
Running/Exploring the Program

