Problem Description
Place a coin on any unoccupied star point connected to
another unoccupied star point and move it to the other end. Can you do
this 6 more times so that 7 of the star points are occupied?
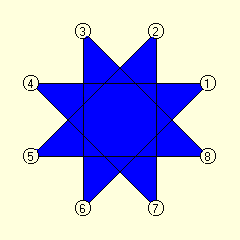
Source: The Master Book of Mathematical Recreations, Fred
Schuh, Dover Pubs., 1968
Background & Techniques
Dec 17,2001 Addendum: Posted a revised
version today that allows user play - and mildly insults you when you lose!
If you want the program and are not interested in the
program logic, just scroll down to the bottom of the page to
download the executable.
This program could be solved by the "brute-force"
method, trying all possible configurations since there are only 7X6X5X4X3X2
(7!) possible arrangements. What I call brute-force, real mathematicians call
"exhaustive search".
However in this case, as in the Knight's Tour puzzle, there is a
selection rule that can "prune" the search tree. In fact, this
rule is probably provable - strong enough that we don't have to worry about
backtracking or retracting bad choices. The rule is to select the unoccupied
star point (vertex) with the fewest free lines
coming into it, where a free line is defined as a line with no coin at
either end.
The first problem is internally representing the
graph. I decided to create a TVertex record for each star point containing it's
display coordinates, whether or not it is occupied, and the number of free lines
coming into that vertex. An array, Vertex, containing 8 of
these records describes the vertices. A second doubly dimensioned array, Lines, contains 8 X2 entries - each of the
eight
1st level indices represents a line and the two 2nd level entries contain the indices of the
end-point vertices. An alternative, and probably better, structure would have each vertex record contain the indices of the two
vertices at the other ends of the lines emanating from it. (e.g. the first
vertex entry would contain the integers 4 and 6 indicating the connected
points). Implementing this change would simplify the code, but
is left as an exercise for you guys.
(Addendum:(Dec. 17, 2001): In
the course of modifying the program to allow user play, I implemented the
above change. So the Lines array no longer exists, but fields C1
and C2 in each Vertex record contain the index values of the
two connected points. This also eliminated the need for the freelines
variable described below. C1 and C2 point directly to the
connecting line ends, so it's an easy matter to see if they are occupied.)
I created a TCoinBoard object, descended from TPaintbox, to
contain board information. The Paint method redraws the board
from Vertex and Lines information as required. There were a couple of
interesting sub-problems in implementing Seven Coins. How do we determine the
number of free lines coming into a vertex? I solved this by initializing
the freelines variable to 2 for each vertex, then finding and reducing freelines
each time a coin was placed, both for the vertex containing the new coin and
those connected to it (if they are unoccupied) .
In order to generate the vertex locations, we divide the 2Pi
radians in a circle by 8 to get the angular displacement from vertex to
vertex, then further rotate the first point by 1/16 of a circle. The
radius is set at some fraction
The other interesting problem was placing the coin. I
decided to animate the placement by displaying the new coin at the center of a free
line and moving it to the vertex location. A TShape defined as a
circle is a simple way to do
this, however I learned that a cannot be the parent of a
control. There are good reasons for this, Windows manages it's real
windows including all Delphi components descended from TWinControl. Since
there are a limited number of of Windows resources available, Delphi has another class,
TGraphicControl, for visual components that require a canvas but not other
window properties.
To make a long story short, by making TCoinBoard the parent of the Coin
TShape, it will automatically be released when TCoinBoard is
freed.
Running/Exploring the Program

