Problem Description
.The object of this puzzle is to arrange the
integers 1 through 16 into a 4x4 grid so that the sum of any two cells
horizontally or vertically is a prime number (no divisors except 1 and
itself).
Background & Techniques
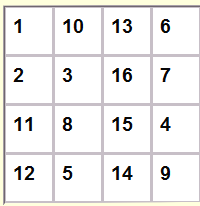
Here is one of the 2992 solutions which can be generated by the
program. Since the only even prime is 2 and the sum of adjacent cells
will always be 3 or greater, all of the prime sums must be odd. And, since
the sum of two even or two odd numbers is always even, it is clear that each
number must have neighbors of the opposite parity. If a row contains
odd-even-odd-even numbers, the row above or below must contain
even-odd-even-odd numbers. The effect is similar to a checkerboard with
number of one parity on the black squares and numbers of the other parity on
the red squares.
No user play is included in the program, so you're on your own if you want
to try discovering a solution without help.
The puzzle was adapted from "The Master Book of Mathematical Recreations",
Fred Schuh, Dover Publications. The book has several pages describing
techniques for finding solutions manually. The book is out of
print, but you can use the Amazon link in the sidebar at left to find used
copies.
The program takes advantage of the "checkerboard" arrangement of odds and
evens by permuting the 8
odd numbers into the "odd" positions and for each of those, permuting the 8 even
numbers into the "even" positions and then checking for prime pair sums. For
a second "Solve" button, the odd-even roles are reversed. Note that if the effects
of rotating and mirroring are considered, the number of unique solutions is
reduced by a factor of 8.
Non-programmers are welcome to read on, but may
want to skip to the bottom of this page to download
executable version of the program.
Notes for Programmers
Upon first reading the problem description, it seemed to be quite
trivial, just generate all permutations of the integers 1 to 16 and check the
sums appropriately. For the 12 horizontal
pair sums,( positions 1, 2, 3, 5, 6, 7, 9, 10, 11, 13, 14, 15), sum with
the next number and check to see if the sum is prime. For positions 1 through 12, check the
vertical pairs by summing the number in
that position with the one 4 positions later (position 1 + position 5,
pos. 2 + pos 6, etc.).
The problem is that there would be 20 trillion permutations to check (2x1013).
A little further thought made it clear that there is no need to check all
permutations. As explained above, odd and even numbers must be
adjacent, so we can permute the odds and evens separately and insert them in
an array appropriately to perform the sum check. There are "only"
40,000 permutations of 8 objects, so we can get by with checking (4 x
104) 2 = 1.6 x 109 permutations,
reducing the problem size by a factor of 10,000 and allowing solutions to be
found in a minute or less on a modern computer.
Once an array is ready to be checked, the fastest way turned out to be
testing that a sum was not one of the five non-prime odd numbers between
the smallest sum (1+2=3) and the largest (15+16=31). The
non-primes in this range are 9, 15, 21, 25, and 27. Finding any
of these values among the 24 sums to check allow us to stop checking that
array immediately.
The MathsLib unit is included in the downloadable source zip file.
It contains the NextPermute function used to generate the
permutations. The MathsLib version included in DFFLibV13
has NextPermute code in the Implementation section but omitted
from the Interface section. That will be corrected in the next
library release.
By the way, in case you haven't caught on to the trick to converting a
one dimensional array into a two dimensional grid, here's a small table
converting 8 array entries into a 4 column x 2 row grid using mod
(modulo) and div (integer division) operations.. Note that all
numbering starts a 0. This is the default for most table indexing because it
simplifies the math. If you are given or prefer to number from 1 as
most humans do, then it's a matter of subtracting 1 from the position
before doing the "mod" or "div" operation and adding 1 back to
the result if necessary.

