Problem Description
Here's the email which prompted this program:
Contact requested
I have a puzzle that's bugged me for a long time. This is probably just
my failure to learn enough math.
A-----------B
| |
|
E ---- F---G
| |
|
D-----------C
Given a bounding rectangle defined by points A,B,C,D;. Point F is a
point in the absolute middle of the bounding rectangle, given half way
between AB and BC. Point E is half way between A and D. Point G is half
way between B and C. The last variable is an angle THETA from 0-360 that
is based upon the line FG, where 0/360 is defined by the line of FG and
180 is defined by FE.
The puzzle is how to create a formula to define a line that will always
intercept point F using angle THETA, but will also define the two X,Y
coordinate points where the line will intercept the perimeter of the
bounding
rectangle. For instance, if angle THETA was 0, 180 or 360, the line
would intercept at points F and G.
If this is an easy one for people.. I'm gonna go back to school. All my
solutions had some random error, but it might be due to my need to
convert back & forth from radians.
Background & Techniques
Here's the derivation of an algorithm that
will provide the answer. First a more concise statement of the
problem:
Determine which side or sides of a given
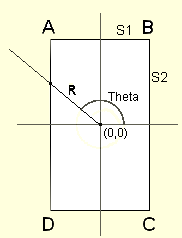
rectangle are intersected by a ray from the center at a given angle.
Assume that the center of rectangle ABCD is at coordinates (0,0) and let
S1=length(AB)/2 and
S2=length(BC)/2 and
the ray extends from (0,0) at angle theta (q),
intersecting the rectangle at distance R
Then the equations for the lines containing the sides can be defined as
follows:
For AB: Y=S2, with -S1<=X<=S1
for BC: X=S1 with -S2<=Y<=S2,
for CD: Y=-S2, -S1<=Y<=S1 and
for DA: X=-S1, -S2<=Y<=S2
The intersection coordinates for the ray line at angle
q can be defined as X=R*cos(q)
and Y=R*sin(q) with R
being the distance from the center at (0,0) to the point of
intersection.
Let's derive the intersection point for the ray and side AB
-------------------------------------------------------------------------------------
Y=S2 and because Y=R*sin(q), we
can divide and define R as R=S2/sin(q).
Substituting for R in the ray equation for X we have
X=(S2/sin(q))*cos(q))
or by rearranging terms
X=S2*(cos(q)/sin(q)).
Cos(q)/sin(q)
is the definition of cotangent(theta) so X can also be caculated as
X=S2*cotan(q)
The above equations do not take into account that we are checking a line
segments, not lines of unlimited length, so we need the extra
checks to make sure that the intersection point is within the bounds of
AB (Y is between
-S1 and +S1) and that we are not talking about the
"backend" of the ray (angle must be between -90 (or 270)
and +90 degrees. And we need to detect and not try to evaluate
the special case when the ray happens to be
parallel to AB. It will never intersect and the cotangent
function is undefined (because the divisor, sin(q),
has
value 0.
Similar analyses can be applied to the other three sides to determine
the point or points of intersection for the ray. It will intersect
2 adjacent sides if it happens to pass exactly through a corner of the
rectangle.
The sample program allows you to set the lengths of the sides of the
rectangle and the angle of the ray. It draws an approximate image
of the resulting figure and displays which side or sides are intersected
by the ray.
Notes for Programmers
The code to derive the intersection coordinates is a straightforward
implementation of the above description. The main addition is to
draw the diagram to visually show the rectangles and the ray as the
parameters are changed by the user. A procedure DrawRect
is called which uses a TImage canvas to redraw the rectangle,
label the corners and draw a line from the center to a point just out
side of the rectangle. A common OnChange exit,
ValueChange, is called each time one of the 3 TSpinedit
values (ABlength, CDlength, ThetaDegrees) changes.
There is a bug, or at least deficiency, in Delphi's
TSpinedit code when typing rather than using the up-down arrows is
used to change the value. It attempts to convert the blank text
field to an integer using Try-Except logic. This works OK
unless we are running in Design mode when the EConvertErrors
interrupt the execution to report the error. It "bugs" me,
so I check for a blank Text property and exit if true at the
start of the ValueChange procedure.
One more programmer's trick at the beginning of ValueChange.
The initial text describing the program is initially displayed in the
same TMemo where the intersection results are displayed after
each parameter change. On initial entry I want to display the
results without clearing that introductory text. I do that by
calling ValueChange in the FormActivate method, but
checking the Sender parameter at the beginning to see who caller
was and only clearing the TMemo when the caller was one of the
TSpinedit controls.
Running/Exploring the Program

