Problem Description
A program to solve sets of equations (N equations
with N independent variables), using Newton-Raphson method of successive
approximation.
Background & Techniques
 |
Sample case:
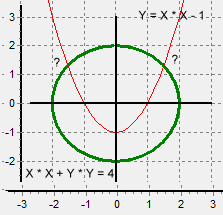
Circle, Parabola Intersection |
Every student who has had a math class that included the word term
"derivative", has probably used Newton's method to calculate the square root
of 2. See the excellent
Wikipedia article
for a refresher. The extension of this method to sets of equations with
multiple independent variables is completely analogous to the single
variable method if we replace the single variable derivative with the partial derivatives of each of
the functions with respect to each of the variables. The math gets
messier as does defining a user interface to enter the equations, but the
concepts are the same. The best explanation I found for
Newton-Raphson is the set of lecture notes by Dr David Keffer at University
of Tennessee at Knoxville. You can check them out at
http://utkstair.org/clausius/docs/che301/pdf/systems.pdf .
I was motivated to explore the multivariate Newton-Raphson method by my
previous work on Point from
4 Sensors. which defines distance equations for sensors (or satellites)
with known locations to define the location of a target (or GPS receiver).
For demo purpose, the equations in the current program are limited to
quadratic polynomials with 4 or fewer independent variables although it
could certainly be extended to more complex types.
The initial default case solves the equations illustrated above, a parabola
intersecting a circle.
The program allows you to specify the number of variables, N, from
1 to 4, for which you need to supply the coefficients for N equations and
also N initial guesses for variable values which solve the system.
The program handles the business of making successive estimates until the
number of iterations have been tried or, preferably, the estimates
converge close enough satisfying the equations.
You can supply the tolerance; the largest difference between the current
equation values and zero (the exact solution). You can also set
the maximum number of iterations before stopping the execution. In
addition to the Solve button, there are buttons to Save and
Load cases. A few sample cases are included with the
downloads.
Non-programmers are welcome to read on, but may
want to skip to the bottom of this page to download
executable version of the program.
Notes for Programmers
There were two distinct problems to solve when writing this program;
implmenting the Newton-Raphson methed and how to let the user input problems
to be solved.
The more interesting one was implementing the Newton-Raphson method
itself. The NewtonMulti function is contained in unit
UNewtonMulti for portability and has this calling sequence:
Function NewtonMulti(
N:integer; {The number of variables and equations}
MaxIter:integer; {Maximum number of iterations to run}
Tolerance:extended; {The maximum residual values}
var X:TnVector; {The array of initial variable value guesses on
entry, final result values at exit time}
var Iter:integer; {The number of iterations executed}
memo1:TMemo; {A Tmemo where results of each iteration are
displayed, Nil = no display}
CallbackRJ:TGetResidualsAndJacobian {Calculates residuals and next
Jacobian}
):boolean;
The calling program must provide the procedure to calculate the array of
Residuals, the result when the current variable estimates are plugged into
the functions, and the Jacobian matrix, the array of partial derivative for
each function with respect to each variable. With these two
pieces of data, NewtonMulti can calculate the next set of variable
estimates, XN+1 = XN - (JN)-1RN.
I.E. the next estimates are calculated as the previous estimates minus the
changes in variable values which would be solutions if the functions were to
proceed to the axis crossing in a straight line with the slope defined by
the partial derivatives. (There, I described it in words, which may
not be much of an improvement over saying it in math symbols .
There's an excellent paper by an engineering professor at University of
Tennessee Knoxville but which currently seems to be unreachable. I'm
trying track it down and will post a link here when I do.)
The second problem, user interface, I solved by restricting systems
analyzed to order 4 or less quadratic polynomials. That still requires
up to 36 inputs for which Iused TEdit controls in an
array with the Tag properties indicating the row and column to which
each refers. (Row = Tag div 10 and Col = Tag mod 10).
With a little fancy footwork turning off the Visible properties
for variables and equations not applicable for the current number of
variables, it seems to work OK. All of the coefficient changing takes
place in a separat dialog, CoeffDlg, in unit U_CoeffDlg.
Values are transferred to arrays JacX2Coeff and JacXCoeff
containing the squared and linear coefficients for each variable of each
equation with vector JacConst containing the constant terms for
each. .The type definition for these arrays and vectors are contained
in the included UMatrix unit. UMatrix encapsulates
the old Borland Turbo Pascal Numeric Toolbox unit and contains
one or two matrix operations used here as well.
Running/Exploring the Program

