Problem Description
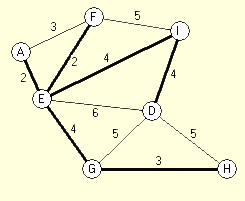 Here's
a program to test whether Kruskal's algorithm for finding minimal spanning
trees for a connected graph really works. (It does.)
User's can interactively add, delete, and move nodes; connect nodes
by edges; assign weights and delete edges; and save and reload graphs
built in this manner. Oh, and display the minimal
spanning tree by clicking a button.
Here's
a program to test whether Kruskal's algorithm for finding minimal spanning
trees for a connected graph really works. (It does.)
User's can interactively add, delete, and move nodes; connect nodes
by edges; assign weights and delete edges; and save and reload graphs
built in this manner. Oh, and display the minimal
spanning tree by clicking a button.
(June 29, 2007: A
second method for finding minimal spanning trees, Prim's Algorithm, was
added today.)
Background & Techniques
Some time ago I wrote a Delphi class (TGraphList) to handle
graph objects and which includes depth first and breadth first searches
for paths connecting two nodes and Dijkstra's algorithm for finding the
shortest path between two nodes. That was largely motivated to help
solve some large search programming problems proposed in
ProjectEuler.net. A recent problem requires finding a
"minimal spanning tree", and was a logical extension to
TGraphList. This program is a version of the result.
I decided to add some graphics features, so nodes now optionally
include x, y coordinates.
Some Graph Definitions
Here is brief set of definitions leading to the one main interest
here, minimal spanning trees.
Graphs consist of nodes (also called vertices),
logical objects of most any sort, and edges, logical connections
between pairs of nodes. Edges may have weights associated
with them. Graphs
Multivariate Newton-Raphsonare a valuable data structure for solving
many types of problems including puzzles and games where nodes can
represent states of the board or puzzle and edges are moves which can get
us from one state to another.
A path is a set of edges leading from one node to another. There
may be more than one way to accomplish this. A graph is connected
if there is a path from every node to every other node. A simple
path is a path which has no nodes repeated. A cycle is a
simple path except the first and last nodes are the same. (As
an aside, a cycle which includes all of the nodes in a graph is called a Hamiltonian
Cycle, Hamiltonian Circuit, Hamilton Cycle, or Hamilton
Circuit.)
Continuing down our main road, a tree
is a set of nodes which contains no cycles. There is only one way to
get from any node to any other node in a tree. A spanning tree
is a tree that includes all of the nodes in a graph. A connected
graph contains at least one spanning tree. Finally, for our
purposes, a minimal spanning tree is the spanning tree the sum of
whose edge weights is less than or equal to the sum of the weights of any other
spanning tree for this graph. If nodes represent cities
and edge weights represent distances, and we need to run trunk power lines to
each city, the minimal spanning tree will define the minimum total miles
of line required. Notice, by the way that, for physical travel,
trees
are not the solution since they not consider the distance to return from any
dead end branch of the tree. For routing problems (mail routes,
school busses, garbage trucks, and traveling salesmen), other path
types provide a better approach. And present a much harder problem.
Operation .
The program operation should be quite self explanatory so I won't waste our time with a click by click explanation.
Clicks on empty spaces on the image field will add a vertex to the
graph. Clicks on existing vertices or edges will pop-up a menu of
available actions.
For now, there is a restriction on node names - they are assigned
as single letters and may not be changed or
reused once assigned, although they they may be moved or deleted. This
means that no graph defined in this program can contain more than 26 nodes .
Non-programmers are welcome to read on, but may
want to skip to the bottom of this page to
download executable version of the program.
Notes for Programmers
TGraphList
Adding graphic capabilities to TGraphList
meant adding x, y coordinates to nodes. No actual graphic output was
implemented, I kept that in the main unit U_MinimalSpanTrees.
For efficiency in handling large graphs, the original TGraphList required
all nodes be added before the edges. The nodes were
"finalized" by sorting them and this allowed the edges to
contain only index pointers to the nodes representing the
ends. That structure is not the best for interactive graph
building where nodes and edges may be added and deleted in any
order. The compromise solution is to add node ids in increasing
sequence, i.e. the id of a deleted node is not reused. This
eliminates the need to re-sort when a node is added, which is not the case
for batch mode problems where nodes may be added in any order. It
also means that, for now, change to node Ids is not allowed.
UGeometry
Since we allow changes to edges, a CloseToEdge
function was added which in turn required calculating the perpendicular
distance from a (clicked) point to a line (edge). Function PerpDistance
was added to a new UGeometry unit for this purpose. In the
process, I discovered that the Intersect routine called by
PerpDistance doesn't work well for lines near vertical. I
replaced it with LinesIntersect from another
program. Fixing Intersect is another project for the futures
list
File Streams
The only other item of interest that comes to
mind is the use of file streams to save and restore graphs. In
particular I had to re-learn how to save a string in a stream. I'll describe
it so I might find it here the next time the need arises. (Save the
length (Len) of the string (S) to the stream first, then save Len characters from
S[1]. At load time, read the length (Len) of the string (S), use
SetLength to set the length of S to Len and then read Len characters into
S[1]).
Two units, UTGraphSearch containing TGraphList and UGeometry
containing several computational geometry functions, were added to
our DFF Library file so these units are not included in the zipped source
file for MinimalSpanTrees. The library reduces the number of files
to be reposted when one of its units changes. (One library file as
opposed to many program source zip files which use the changed unit).
Addendum June 29, 2007: A young
Chinese student had an assignment to explain both Prim's and
Kuskal's Algorithms for finding minimal spanning trees (MST) using code
samples from any source. To help him out, I added a Prim's button
to the the MST program today. It is actually predates
Kuskal's method, is simpler, and slower. The algorithm
assigns any node as the first node of the tree and then loops looking for
the node not in the tree with the smallest weighted edge to a node in
the tree. That node is added and the loop begins again. The
search continues until all nodes have been added.
Running/Exploring the Program

