Problem Description
Genaille's Rods, also called Genaille-Lucas Rulers, are
an extension of a graphical method of multiplying and dividing developed by
Napier in the 16th century. I thought they were kind of cool - so
decided to develop a program to make a printable version. This is it.
Reference: Knotted Doughnuts, Martin
Gardner, W. H. Freeman & Co.
Background & Techniques
Baron John Napier gave the world it's first table of
logarithms and coined the word logarithm. In the days before calculators,
methods of simplifying calculations were of much interest. In 1617 Napier
also published a book describing a method to multiply, divide and extract square
roots using a set of bars or rods. These became known as Napier's
Bones.
In the late 1800s, Henri Genaille, a French civil
engineer, invented an improvement to Napier's Bones that eliminates the
need to handle carries from one digit position to the next. The problem
was posed by Edouard Lucas and thus the alternate name of Genaille-Lucas Rulers
.
The process of multiplying any integer of any
length by a digit 1-9 is reduced to looking up numbers on the rods.
Studying how and why these rods work gives real insight into the nature of
multiplication.
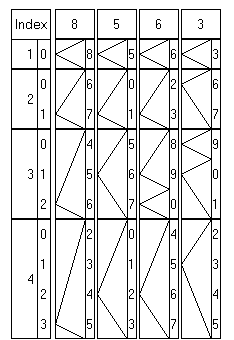
Here's an example which shows partial rods set up to
multiply 8563 by a digit from 1 to 4. Starting from the rightmost,
topmost digit for a particular index value, the answer can be read directly by
following the arrows to the left. For example 8563 X 4 is 34252
The program has over 400 lines of source code,
which puts it in the Advanced category per my arbitrary classification
system. However a couple of hundred lines handle various display options
that were implemented for debugging (draw a single box, draw a single row, draw
a single rod, etc.) so I'm calling it an Intermediate. The
heart of the code is an exercise in drawing directly on a canvas. By
displaying the image in a TImage, we can let the component worry
about redrawing the image as required.
A simple TRodSet object is defined to hold the basic parameters used
while drawing rods. TRodSet.DrawBox is
the key procedure - it displays a particular multiplier/multiplicand box at a
given set of coordinates - and was the most fun to write.
The print routine draws directly on the printer
canvas. If memory is limited (for example on my old Dell laptop) -
an "out of resources" error may occur. There's some
commented code that I used to draw the image on a half size bitmap and StretchDraw
it full-sized to the printer canvas in this case.
Running/Exploring the Program

