
Search

As of October, 2016, Embarcadero is offering a free release
of Delphi (Delphi
10.1 Berlin Starter Edition ). There
are a few restrictions, but it is a welcome step toward making
more programmers aware of the joys of Delphi. They do say
"Offer may be withdrawn at any time", so don't delay if you want
to check it out. Please use the
feedback link to let
me know if the link stops working.

Support DFF - Shop
If you shop at Amazon anyway, consider
using this link.
We receive a few cents from each
purchase. Thanks

Support DFF - Donate
If you benefit from the website, in terms of
knowledge, entertainment value, or something otherwise useful,
consider making a donation via PayPal to help defray the
costs. (No PayPal account necessary to donate via credit
card.) Transaction is secure.

Mensa®
Daily Puzzlers
For over 15 years
Mensa Page-A-Day calendars have provided several puzzles a year
for my programming pleasure. Coding "solvers" is most fun,
but many programs also allow user solving, convenient for "fill
in the blanks" type. Below are Amazon links to the
two most recent years.
Mensa®
365 Puzzlers Calendar 2017
Mensa®
365 Puzzlers Calendar 2018

(Hint: If you can
wait, current year calendars are usually on sale in January.)

Contact
Feedback:
Send an
e-mail with your comments about this program (or anything else).

|
| |
Problem Description
Drag the lettered blocks onto the template to form valid words reading across
and down crossword style. No need to rotate pieces and each piece is used
exactly once. Here's what the downloaded puzzle looks like:
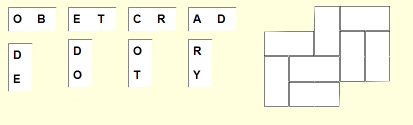
Background & Techniques
The puzzle is the first and only example of this type I've found in my many
years as a fan of the Mensa "Puzzle-A-Day" calendars. It's from the June
18, 2010 puzzle page.
To play, drag and drop blocks onto the template, horizontal blocks onto
horizontal spaces and vertical blocks onto vertical spaces. To replace a block
drag the incorrect block anywhere off of the template. Use the "Hint"
button for a littler help if you get stuck.
A future version will add dictionary lookup capabilities so that many additional
valid puzzles can be generated (I hope!).
Non-programmers are welcome to read on, but may want to jump to bottom of
this page to download the executable program now.
Programmer's Notes:
Job 1 for implementing a computer model of a real world object (this puzzle,
for example), is to determine the data structures which will let us
describe and manipulate the parts. In this case, TStringGrid
controls are logical candidates for the lettered blocks and the board template
which controls where the blocks can be placed. Using Delphi's
ability to define new classes, I defined a TBlock class as a TStringGrid
descendent with a few additional fields. Namely
 | Rank - What is my index number? |
 | PositionOnBoard - Am I on the board (-1 if not). If so, where on
the board am I? |
 | SolutionIndex - Where on the board should I be when puzzle is solved? |
 | HomeX, HomeY: What were my original pixel coordinates (so I can return
here later if necessary) |
There's an array, Block, of TBlock controls defining the 8
blocks. Each block gets a lot of information from 8 TStringGrid
controls that I defined using Delphi's visual design capabilities. See
TBlock.Create and TBlock.Assign for the details. This allows us
to reference any of the blocks using common code referencing Block[i].
Setting the Dragmode property to dmAutomatic allows the blocks to
be dragged using the mouse. The board . template, named Board, is a
5 x 4 TStringGrid which has OnDragOver and OnDragDrop exits
to allow properly oriented block to be dropped on it.
In order to identify where the blocks can land and where they should be when
the puzzle is solved I defined a 3-dimensional BlockMap array [0..4,
0..3, 0..1] containing two integer values for each of the 5 columns and 4
rows of the template grid. The first digit is simply an index number
assigned to each block target location, '0' to '3' for the horizontal blocks and
'4' to '7' for the vertical blocks. The four top left and bottom right
cells are assigned a value of '-1 to indicate that no block can be dropped
there. The second digit for each cell contains an offset value of '0' for
the top left cell of each block and '-1' for the other cell for each
block. This way, when the user drops a block on the board, the drop cell
plus the offset value will point us to the first cell of the block.
Here's how BlockMap identifies the block locations:
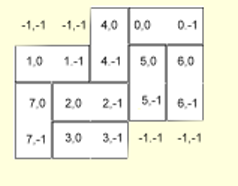
How do we use Blockmap?
- The OnDrawCell exit for the Board get passed a column and
row to draw each cell where we want to draw an outline of the the left or
right end of a horizontal block or the top or bottom for a vertical block.
The exit uses the BlockMap data to determine how to outline that
cell.
- When the user drags a block over the board, an OnDragOver exit
must set an "Accept" Boolean variable to true or false to
control whether the block can be dropped at that location. BlockMap
provides it with the necessary information.
- When the user drops the block on an acceptable location, we move the top
left corner of the block to the top left corner of the template location.
The first BlockMap value for the drop cell tells us whether it is a
horizontal or vertical block (<=3 for horizontal) and adding the second
index value to the column (for horizontal blocks) or row (for vertical
blocks), makes sure that they address the top left corner of the proper
cell.
- BlockMap provides the PositionOnBoard value to plug into
the Block record for a dropped block. The SolutionIndex
was filled in for each block when the case was defined so it becomes a
simple matter to run through the block and check if all are in the correct
location. If they are, give the user a "Congratulations" message.
- When the Hint button is clicked, we want to either remove one
block that is in on the board but in the wrong location or move a
random unplaced block to the correct location on the board.
BlockMap will tell us where the correct location is. (For block N,
scan Blockmap looking for the cell entry containing data [N,0].
Another slightly tricky bit is converting clicked pixel positions to cell
locations. The TStringGrid MousetoCell method does this for
us. When we drop a block on the board, we also use the Cellrect
method to determine exact pixel values on which to drop the block.
There's probably some other stuff that needs describing, but it's getting
late. As usual, use the feedback link to ask if
you have questions or suggestions.
Running/Exploring the Program
Suggestions for Further Explorations
 |
Add our dictionary unit to the program so that
additional puzzles could be created. We'd probably want to add
Save and Load capabilities. |
 |
.Could arithmetic
versions be created? |
 |
Other puzzle sizes? |
| Original: August 6, 2010 |
Modified:
May 15, 2018
|
|

