Problem Description

"Hi I have been searching the internet for a trick using square cards  (or paper) with numbers and holes in them. The trick was to choose any  number on the cards and one at a time turn each card to "yes" or "no"  written on each card depending what cards have that number. after that  the pile is to be turned over and the chosen number is shown through a  hole on the bottom of pile. Do you know How I might search the internet for this?

Any help would be appreciated.

Thanks,   Peter

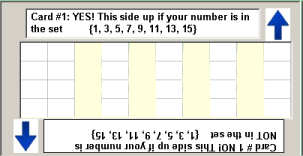
Background & Techniques

It seemed clear that this was a binary coding trick.  I decided to implement a sample set but with some modifications.  The final card of the deck described by Peter probably had all of the numbers on it with the word "YES" and the numbers printed again on the back of the card in specific positions.  This card would always be the last card placed on the stack of "YES" cards and therefore , when turned over, be on the bottom with the numbers on it's back side showing through anywhere there was a hole in that location on every  card.   My card with all of the numbers on it will lie face up and have the Yes/No cards laid on top of it.

Peter couldn't remember where the words "YES" and  "NO" were written or what type of rotation was required.   But the idea will be to align N cards (for numbers in the range 0 to 2^N-1)  and with the holes in each representing the 0 and 1 bits for a specific bit position for the numbers printed on that card.

I chose to use the top half of the rows on each card for the "0" bits and the bottom half for the '1" bits.  Rotating the "No" cards by 180° will then move the "0" bits to the bottom half to line up with the "1" bits in the same position on the "Yes" cards. (Note that if we fill in the "1" bits in increasing numeric order, the "0" bit rows must be reversed since rotating will reverse them again.)

As a simple case, assume we are implementing the trick for numbers {0,1,2,3}, 2^2.  In binary {00, 01, 10, 11} so our cards could look like this:

Now we need a card for each bit position, in this 0 to 3 case,  the right bit (1's position) card and the left bit (2's position) card and.   From the way the the numbers are laid out the base card, we can determine which squares must be cut out and which must be left closed for each row and column on each card.  Label the cards with the numbers which have that card's bit position turned on in their binary representation.  Then cut out the squares in the bottom row which will line up with those numbers as printed on the base card.  Now rotate the card 180 degrees so that the "NO" side is up and cut out all of squares in the new bottom row except those which would let any of the numbers n this card show through.    Not a very clear explanation I'm afraid, but I can't seem to figure out how to say it better. Here's what the cards would look like:

 
  Left  bit card▲          Right bit card▲

The top row with 4 cells represents the "0" bits in the binary representation of the 4 numbers , but since we will invert the cards that have a 0 in that position, we must fill in the holes in reverse order (inverting will put them back in the correct order).   The 2nd row with 4 cells has holes for the numbers with "1". 

And we could, of course, label the base card with symbols {1 2 3 4} or (A B C D} or {chicken, cow, horse dog} or any symbols we choose so long as the Yes/No cards are labeled appropriately.

The sample program which can be downloaded below expands this idea to numbers 0 to 15 by including 4 rows with holes, two rows for "0" bits and two for "1" bits just to keep the cards from getting too long.

In operation, I included arrow symbols which rotate the cards to bring the No message to the top.   Click and drag on the grid will let you drag the cards to the Base Card position to see the results.   

A "Reset" button moves the cards back to their original configuration.  A "Print" button prints the form for anyone who wants to make a physical set to prove to themselves that the program (hopefully) works. 

Non-programmers are welcome to read on, but may want to skip to the bottom of this page to download executable version of the program.

Notes for programmers

A good programming exercise here with several complications.

Programming is so humbling!  If you ever get to feeling quite smart, just try a program that has to emulate some task that is simple and natural for the human brain (like turning a cord over or placing it on a stack).

Addendum December 19, 2007: An update was posted to day to improve the visual layout of the the cards. 

Running/Exploring the Program 

Suggestions for Further Explorations