[Home]
We can tell that the Olympics are here - the Olympic Rings puzzle program page has been the most visited DFF website for the past month or so, now averaging over 600 visits per day! I'm sure that most people are not looking for an Olympic Rings puzzle, but a small percentage wander on to other pages on the site, so maybe one or two will become Delphi programmers.
By the way, the Olympic Rings stats came from a daily statistics report for the website. I posted yesterday's report at http://delphiforfun.org/DFF_daily_stats.htm. We had visitors from 40 states, 6 Canadian provinces, and 56 countries - a pretty typical day. Maybe some math teachers can use it to pose some interesting statistics problems.
We visited the Destination Imagination Global Finals at the end of May. It is easy to get discouraged by world events these days, but seeing the some of our brightest youth in action renews one's faith in the future. An uplifting experience.
You'll find information below about "Kirkman's 15 Schoolgirls Problem". It's one of those "easy to state, hard to solve" problems that I really like. And this one has been a challenge. I have posted a program that finds lots of solutions, but , so far, identifying the seven unique solutions eludes me. One of of these days (or weeks, or months), I'll crack it.
May 22, 2004: I ran across the following problem recently in my daily Mensa® Puzzle calendar;
Find the six digit number in which the first digit is one less than the second and one half the third, the fourth digit is one more than the third and is also the sum of the first and second, and the the fifth and six digits make a number which is the sum of the first four digits. The sum of all the digits is 19.
It's an algebra problem, but I thought I'd try to "Brute Force" it just for fun. Brute Force uses trial and error methods to search for a set of variable values that satisfy a set of equations. Every Brute Force problem to date had a unique value for each variable. This problem has at least one repeated value. which required a small modification to the program. The new version was posted today. A few additional "Brute Force" type problems have popped up since the last posting so there are now 16 samples included.
 |
|
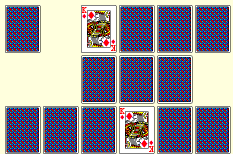
Found another pair! |
May
24, 2004: Here
is my version of the memory card game commonly called Concentration.
The
objective is to form pairs from an array of face down cards by drawing two
cards in each turn. Matched cards are removed; unmatched cards are
turned back face down. When the field is empty, the player
with the most matched pairs is the winner. This version allows one or
two players and setting the deck size from 1 to 20 pairs.
May 25, 2004:
We reached a milestone this week - 200,000 programs downloaded in the past 12 months! Here are a couple of small program changes posted today:-
Permutes2 now allows users to display combinations or permutations of subsets from a set of character strings as well as numbers. (User request.)
-
A viewer pointed out that the MoonDates program would occasionally skip months when listing the dates of new and full moons for a year. I think it's fixed.
May 31, 2004:
We just returned from the Destination Imagination Global Competition in Knoxville, TN. An awesome experience with some awesome kids! Read more about it and see some pictures here.June 9, 2004: I uploaded a revised version today of the DFF Play CD, a file that contains executable versions of 60+ programs from this site. I put it together last December for use in our schools here. The file includes an autorun file to start automatically from a CD but will run fine from a hard drive. There's a loader program, Programload.exe, used to select programs by category (Science, Math, Games, Puzzles, Tricks). If you run it from hard drive or if auto start is not enabled on your PC, start by double clicking the loader program. The zipped DFF Play CD file is about 20mb in size.
I plan future updates with additions, deletions, and enhanced versions, so pertinent feedback with bugs reports or suggestions will be appreciated as always.
In the process of updating the CD, I ran across a few typos and minor bugs. As a result, new versions of Brute Force, Card Trick, and Magic Matrix programs have been uploaded.

June 11, 2004: Here's an update to the Computational Geometry page over in Delphi Techniques section that adds the solution to this problem: . Given a point and a polygon, determine if the point is enclosed by the polygon.
How to do it? Hint: Draw a
long line from the red dot in this image in any direction that doesn't pass
through any vertices. Notice that your line intersects an even number of
polygon edges.
June 14, 2004: I've been trading problems and puzzles with a bright young lady I met at the Destination Imagination finals a couple of weeks ago. She sent me this one the other day: Insert +, -, x, ÷ symbols into the digits 99999 to make an expression that equals 10.
It's not too difficult to find one, but I thought she deserved to see all possible solutions. Besides, I'm trying to convince her programming would be a great career choice. So here is ExpressionsForBethe, which solves not only this problem but similar problems for any given set of digits evaluating to any given value.
 June
17, 2004: Here's a small update to the Scientific
Grapher program with better default values if two series are being
plotted and the ability to control the scale of the dependent variable.
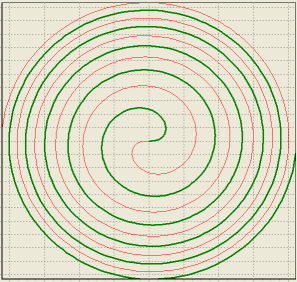
I also added Fermat's Spiral to the sample curve files.
June
17, 2004: Here's a small update to the Scientific
Grapher program with better default values if two series are being
plotted and the ability to control the scale of the dependent variable.
I also added Fermat's Spiral to the sample curve files.
By the way, it has been reported
that practitioners of omphaloskepsis, (contemplating one's navel), use
Fermat's Spiral as their symbol. I'll admit though,
that my search for "Omphaloskepsis" images turned up lots of belly
buttons, but few spirals.

July 7, 2004: For the past several weeks most of my spare programming-for-fun time has been spent working on Kirkman's Schoolgirl problem. I haven't cracked it yet, but I will. It's time to share the problem so that all you hotshot Delphi programmers can try your hand.
Fifteen girls at a boarding school go for a daily walk. In order to prevent cliques from forming, the school mistress has declared that the girls will walk each day in 5 rows of 3 and that each girl will walk in a row with each other girl exactly once. Since each girl must walk aligned with 14 other girls and she walks with 2 different girls each day, it will take seven days to complete the cycle if one exists. The question is how to line the girls up each day to implement the schoolmarm's wishes.
In fact, there are seven distinct solutions to the problem - English amateur mathematician Thomas Penyngton Kirkman published the problem and the solutions in 1850! One DFF viewer, who happens to code in C++, found a brute force solution after about 5 days of CPU time but there are surely more efficient ways. I just haven't found one in Delphi or Pascal yet. There is lots of information on the Web and the solutions are all known, but the journey to finding even one solution should fill lots of pleasant hours. How did Kirkman do it?
 In
the meantime, I posted a modified version of our "Crossword Helper"
word completion program and available from the WordStuff1
page or as part of WordStuff2.
The new version includes an "excluded letters" list to reduce
the number of words returned when a partial word is entered.
Not helpful in solving crosswords, but there is an application in finding
hidden phrases in the "Flip Words" commercial game that seems
to be floating around the web. Viewer Frank, who
probably spends too much time playing the Flip Words, requested the change
because he's addicted and determined to get a high score..
In
the meantime, I posted a modified version of our "Crossword Helper"
word completion program and available from the WordStuff1
page or as part of WordStuff2.
The new version includes an "excluded letters" list to reduce
the number of words returned when a partial word is entered.
Not helpful in solving crosswords, but there is an application in finding
hidden phrases in the "Flip Words" commercial game that seems
to be floating around the web. Viewer Frank, who
probably spends too much time playing the Flip Words, requested the change
because he's addicted and determined to get a high score..
July12, 2004: Here's Kirkman1, version 1 of a program to solve Kirkman's Schoolgirls Problem described last week It finds lots of solutions, but cannot yet determine which are unique and which are merely renamed & rearranged versions of solutions already found,
July 23, 2004: Michael from Demark wrote the other day asking about adding Civil Twilight times to our Solar Position program that has an option to display Sunrise and Sunset times for any date and location. I posted the change today. He's working on a program to display hours of daylight for pilots flying under Visual Flight Rules. They figure that there is enough light to fly when the sun is 6 degrees or less below the horizon.
(Other than that I'm still trying to identify those darn 7 unique Kirkman solutions. I can filter out many, but not enough of the hundreds that the Kirkman1 program produces)
July 27, 2004: This problem was published by Marilyn vos Savant in her "Ask Marilyn" column in the weekly "Parade" magazine last Sunday.
A clueless student faced a pop quiz - a list of 24 Presidents of the 19th century and another list of their terms of office, but scrambled. The object was t match the President with his term. He had to guess every time. On average, how many terms would he guess correctly?
I couldn't figure out how to solve it analytically, so I wrote this simple Random Matching program to find the answer experimentally. 40 lines of code make it a good Beginners level program.
On the Kirkman front - I can now identify the unique solutions! I hope to get the code integrated to make Kirkman2 in the next few days.
August 1, 2004:
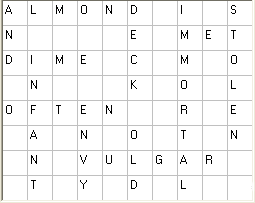 Viewer Dahlia found a bug in our Crossword
Generator program. Non-square boards were
filled only to the limit of the smaller dimension. It's fixed
today. Thanks, Dahlia for "bugging" me until I took the time
from Mr. Kirkman to fix it.
Viewer Dahlia found a bug in our Crossword
Generator program. Non-square boards were
filled only to the limit of the smaller dimension. It's fixed
today. Thanks, Dahlia for "bugging" me until I took the time
from Mr. Kirkman to fix it.
Viewer Charles Doumar sent me a version of the
Kirkman 15 Schoolgirls program that finds solutions much faster than mine.
I added my "uniqueness checking" code to it and it finds the first 6
unique solutions in pretty quickly. The 7th, and final, unique solution
is still hiding after several thousand solutions checked. (Or else we
have a bug -surely that couldn't be!)
August 9, 2004:
![]()
 A
stick is broken randomly into 3 pieces. What is the probability that the
pieces can be assembled into a triangle?
A
stick is broken randomly into 3 pieces. What is the probability that the
pieces can be assembled into a triangle?
Random Triangles answers the question empirically. Perhaps the answer is not what one would think!
http://www.delphiforfun.org/
" If it's not broke, don't break it!" - WinXPNews newsletter
-
To subscribe or unsubscribe from this newsletter, visit http://delphiforfun.org/newsletter.htm
84,000 home page visitors since Sept 2000. 225,000 programs downloaded in the past 12 months!
